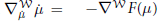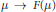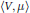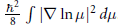We show that the Schrödinger equation is a lift of Newton's third law of motion 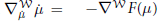$\nabla _{{\dot{\mu }}}^{\mathcal{W}}\,\dot{\mu }\,=\,-{{\nabla }^{\mathcal{W}}}\,F\left( \mu \right)$ on the space of probability measures, where derivatives are taken with respect to the Wasserstein Riemannian metric. Here the potential 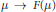$\mu \,\to \,F\left( \mu \right)$ is the sum of the total classical potential energy 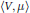$\left\langle V,\,\mu \right\rangle $ of the extended system and its Fisher information 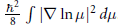$\frac{{{\hbar }^{2}}}{8}\,{{\int{\left| \nabla \,\text{1n}\,\mu \right|}}^{2}}\,d\mu $. The precise relation is established via a well-known (Madelung) transform which is shown to be a symplectic submersion of the standard symplectic structure of complex valued functions into the canonical symplectic space over the Wasserstein space. All computations are conducted in the framework of Otto's formal Riemannian calculus for optimal transportation of probability measures.

Cet article a pour objectif premier d'exposer les méthodes numériquesliées au mouvement de corpsmises en œuvre au sein d'uncode de simulation d'écoulements turbulents de fluides visqueux incompressibles.Une des particularités est de pouvoir traiter, outre les solides classiques,des corps déformables à déformation imposée. On détaillera les techniques utilisées concernant la résolution des équations du mouvement(paramétrage, utilisation d'un quaternion),la gestion du maillage (lié au mouvement et à la déformation des corps)et le couplage écoulement-mouvement. La deuxième partie sera consacrée à la présentation des travaux effectués dans le cadre du Projet Interdisciplinairede Recherche CNRS ROBEA visant à concevoirun robot-anguille autopropulsé à locomotion anguilliforme.Les résultats des premiers calculs tridimensionnels recenséscouplant la résolution de l'écoulement par les équations de Navier-Stokesen moyenne de Reynolds avec le Principe Fondamental de la Dynamiqueappliqué au corps à déformation imposée seront ainsi exposés.