Search

In this paper we are concerned with questions of multiplicity and concentration behaviorof positive solutions of the elliptic problem

$$ (P_{\var})\hspace*{4cm} \left\{ \begin{array}{rcl} \mathcal{L}_{\var}u=f(u) \ \ \mbox{in} \ \ \R^{3},\\[1.5mm] u>0 \ \ \mbox{in} \ \ \R^{3},\\[1.5mm] u \in H^{1}(\R^3), \end{array} \right. $$

(P_{ε}) \{\begin{matrix} ℒ_{ε} u = f (u) in {IR}^{3}, \\ u > 0 in {IR}^{3}, \\ u \in H^{1} ({IR}^{3}), \end{matrix}

where ε is a small positiveparameter, f : ℝ → ℝ is a continuous function, $$ \mathcal{L}_{\var} $$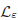 $ℒ_{ε}$ is a nonlocaloperator defined by

$$ \mathcal{L}_{\var}u=M\left(\dis\frac{1}{\var}\int_{\R^{3}}|\nabla u|^{2}+\frac{1}{\var^{3}}\dis\int_{\R^{3}}V(x)u^{2}\right)\left[-\var^{2}\Delta u + V(x)u \right], $$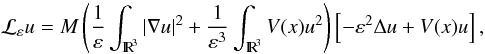

ℒ_{ε} u = M (\frac{1}{ε} \int_{{IR}^{3}} | \nabla u |^{2} + \frac{1}{ε^{3}} \int_{{IR}^{3}} V (x) u^{2}) [- ε^{2} Δ u + V (x) u^{]},

M : IR+ → IR+ andV : IR3 → IR are continuous functions whichverify some hypotheses.

In this paper, we investigate a semilinear elliptic equation that involves multiple Hardy-type terms and critical Hardy–Sobolev exponents. By the Moser iteration method and analytic techniques, the asymptotic properties of its nontrivial solutions at the singular points are investigated.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Multiplicity and concentration behavior of positive solutionsfor a Schrödinger–Kirchhoff type problem via penalization method ∗∗∗

Asymptotic Properties of Solutions to Semilinear Equations Involving Multiple Critical Exponents

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Multiplicity and concentration behavior of positive solutionsfor a Schrödinger–Kirchhoff type problem via penalization method∗∗∗

Asymptotic Properties of Solutions to Semilinear Equations Involving Multiple Critical Exponents

Multiplicity and concentration behavior of positive solutionsfor a Schrödinger–Kirchhoff type problem via penalization method ∗∗∗