1 results
Arithmetically defined dense subgroups of Morava stabilizer groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 247-270
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
-
For every prime p and integer n≥3 we explicitly construct an abelian variety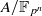
of dimension n such that for a suitable prime l the group of quasi-isogenies of 
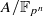of l-power degree is canonically a dense subgroup of the nth Morava stabilizer group at p. We also give a variant of this result taking into account a polarization. This is motivated by the recent construction by Behrens and Lawson of topological automorphic forms which generalizes topological modular forms. For this, we prove some arithmetic results of independent interest: a result about approximation of local units in maximal orders of global skew fields which also gives a precise solution to the problem of extending automorphisms of the p-divisible group of a simple abelian variety over a finite field to quasi-isogenies of the abelian variety of degree divisible by as few primes as possible.
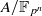of dimension 
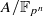of 