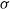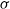1 results
Normal approximation for mixtures of normal distributions and the evolution of phenotypic traits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 162-188
- Print publication:
- March 2021
-
- Article
- Export citation
-
Explicit bounds are given for the Kolmogorov and Wasserstein distances between a mixture of normal distributions, by which we mean that the conditional distribution given some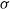
$\sigma$
-algebra is normal, and a normal distribution with properly chosen parameter values. The bounds depend only on the first two moments of the first two conditional moments given the 
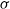$\sigma$
-algebra. The proof is based on Stein’s method. As an application, we consider the Yule–Ornstein–Uhlenbeck model, used in the field of phylogenetic comparative methods. We obtain bounds for both distances between the distribution of the average value of a phenotypic trait over n related species, and a normal distribution. The bounds imply and extend earlier limit theorems by Bartoszek and Sagitov.
