Proper orthogonal decomposition (POD) is applied to three-dimensional (3-D) velocity fields collected from large-eddy simulations (LES) of a baffled stirred tank. In the LES, the tank operates with a Rushton-type impeller under turbulent conditions (at least in the near-impeller region) and the working fluid exhibits either Newtonian or shear-thinning rheology. The most energetic POD modes are analysed, and a POD reconstruction based on the higher modes is proposed to approximate the fluctuating component of the velocity field. Subsequently, the POD reconstruction is used to identify vortical structures and characterise them in terms of their shape. The structures are identified by considering a frame-invariant formulation of a popular, Eulerian, local-region-type method: the 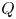 $Q$-criterion. Statistics of shape-related parameters are then investigated to address the morphology of the structures. It is found that: (i) regardless of the working fluid rheology, it seems feasible to decompose the 3-D field into its mean, most energetic periodic and fluctuating components using POD, allowing, for instance, reduced-order modelling of the energetic periodic motions for mixing enhancement purposes, and (ii) vortical structures related to turbulence are mostly tubular. Finding (ii) implies that, as starting point, phenomenological models for the interaction between fluid particles (drops and bubbles) and vortices should consider the latter as cylindrical structures rather than of spherical shape, as classically assumed in these models.
$Q$-criterion. Statistics of shape-related parameters are then investigated to address the morphology of the structures. It is found that: (i) regardless of the working fluid rheology, it seems feasible to decompose the 3-D field into its mean, most energetic periodic and fluctuating components using POD, allowing, for instance, reduced-order modelling of the energetic periodic motions for mixing enhancement purposes, and (ii) vortical structures related to turbulence are mostly tubular. Finding (ii) implies that, as starting point, phenomenological models for the interaction between fluid particles (drops and bubbles) and vortices should consider the latter as cylindrical structures rather than of spherical shape, as classically assumed in these models.