Let F be a field, let G = Gal(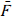 /F) be its absolute Galois group, and let R(G,k) be the representation ring of G over a suitable field k. In this preprint we construct a ring homomorphism from the mod 2 Milnor K-theory k*(F) to the graded ring grR(G,k) associated to Grothendieck's γ-filtration. We study this map in particular cases, as well as a related map involving the W-group
/F) be its absolute Galois group, and let R(G,k) be the representation ring of G over a suitable field k. In this preprint we construct a ring homomorphism from the mod 2 Milnor K-theory k*(F) to the graded ring grR(G,k) associated to Grothendieck's γ-filtration. We study this map in particular cases, as well as a related map involving the W-group 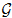 of F, rather than G. The latter is an isomorphism in all cases considered.
of F, rather than G. The latter is an isomorphism in all cases considered.
Naturally this echoes the Milnor conjecture (now a theorem), which states that k*(F) is isomorphic to the mod 2 cohomology of the absolute Galois group G, and to the graded Witt ring grW(F).
The machinery developed to obtain the above results seems to have independent interest in algebraic topology. We are led to construct an analog of the classical Chern character, which does not involve complex vector bundles and Chern classes but rather real vector bundles and Stiefel-Whitney classes. Thus we show the existence of a ring homomorphism whose source is the graded ring associated to the corresponding K-theory ring KO(X) of the topological space X, again with respect to the γ-filtration, and whose target is a certain subquotient of H*(X, F2).
In order to define this subquotient, we introduce a collection of distinguished Steenrod operations. They are related to Stiefel-Whitney classes by combinatorial identities.

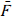 /F)
/F)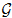 of
of 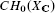 constructed in [L2], we develop and describe geometrically a series of Hodgetheoretic invariants Ψ
constructed in [L2], we develop and describe geometrically a series of Hodgetheoretic invariants Ψ