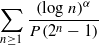Search

Let P(k) be the largest prime factor of the positive integer k. In this paper, we prove that the series is convergent for each constant α<1/2, which gives a more precise form of a result of C. L. Stewart [‘On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers’, Proc. London Math. Soc.35(3) (1977), 425–447].

We give estimates for exponential sums of the form $\sum_{n \leq N}\Lambda(n)\exp(2 \pi i a g^n/m)$, where m is a positive integer, a and g are integers relatively prime to m, and $\Lambda$ is the von Mangoldt function. In particular, our results yield bounds for exponential sums of the form $\sum_{p \leq N}\exp(2 \pi i a M_p/m)$, where Mp is the Mersenne number; $M_p=2^p-1$ for any prime p. We also estimate some closely related sums, including $\sum_{n \leq N}\mu(n)\exp(2 \pi i a g^n/m)$ and $\sum_{n \leq N}\mu^2(n)\exp(2 \pi i a g^n/m)$, where $\mu$ is the Möbius function.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

ON THE LARGEST PRIME FACTOR OF THE MERSENNE NUMBERS

Exponential sums over Mersenne numbers

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

ON THE LARGEST PRIME FACTOR OF THE MERSENNE NUMBERS

Exponential sums over Mersenne numbers