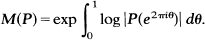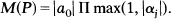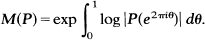1 results
A Measure for Polynomials in Several Variables
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 2 / 01 June 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-191
- Print publication:
- 01 June 1984
-
- Article
-
- You have access
- Export citation
-
We define a notion of measure for polynomials in several variables, basing our construction on the geometry of the zero-set of the polynomial. For polynomials in one variable, this measure reduces to the usual one. We begin the development of the theory of this measure along lines parallel to the theory of Mahler’s measure, indicating the differences and similarities between the two.
Let P be a polynomial in one variable with complex coefficients, P(z) = a0Π(z - αj). The measure of P, denoted M(P), is defined by
1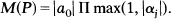
As is well-known, an application of Jensen’s formula yields
2
