1 results
The limit distribution for maxima of ‘weighted' rth-nearest-neighbour distances
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue 2 / June 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 344-354
- Print publication:
- June 1982
-
- Article
- Export citation
-
Let X1, X2, · ··, Xn be independent identically distributed random points with common density f(x), taking values in a bounded region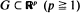
(p ≧ 1). We obtain the limit distribution, as n → ∞, for the maximum value of the suitably ‘weighted' (according to f(x)) rth-nearest-neighbour distances of Χ1, · ··, Χ n (r ≧ 1 fixed) provided that f(x) is bounded from below by a positive constant and a weak continuity condition holds. This is achieved by refining an argument used by the author (Henze (1981)) to derive the limit distribution in the special case r = 1. Edge-effects are eliminated by defining, for each Xi, the distance to the boundary of G to be the ‘rth-nearest-neighbour distance' if it is smaller than the distance to the rth nearest neighbour among the remaining points. Applications to a multivariate test of goodness of fit are given.
(