1 results
Convergence to stationary state for a Markov move-to-front scheme
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 768-776
- Print publication:
- September 1995
-
- Article
- Export citation
-
This work considers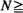
items (e.g. books, files) arranged in an array (e.g. shelf, tape) with N positions and assumes that items are requested according to a Markov chain (possibly, of higher order). After use, the requested item is returned to the leftmost position of the array. Successive applications of the procedure above give rise to a Markov chain on permutations. For equally likely items, the number of requests that makes this Markov chain close to its stationary state is estimated. To achieve that, a coupling argument and the total variation distance are used. Finally, for non-equally likely items and so-called p-correlated requests, the coupling time is presented as a function of the coupling time when requests are independent.
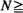items (e.g. books, files) arranged in an array (e.g. shelf, tape) with 