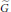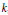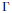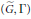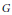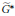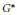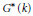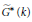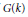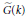Suppose that 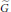$\widetilde{G}$ is a connected reductive group defined over a field 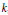$k$, and 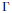$\Gamma$ is a finite group acting via 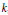$k$-automorphisms of 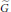$\widetilde{G}$ satisfying a certain quasi-semisimplicity condition. Then the identity component of the group of 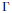$\Gamma$-fixed points in 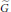$\widetilde{G}$ is reductive. We axiomatize the main features of the relationship between this fixed-point group and the pair 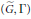$\left( \tilde{G},\Gamma \right)$, and consider any group 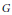$G$ satisfying the axioms. If both 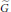$\widetilde{G}$ and 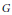$G$ are 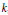$k$-quasisplit, then we can consider their duals 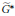$\widetilde{{{G}^{*}}}$ and 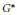${{G}^{*}}$. We show the existence of and give an explicit formula for a natural map from the set of semisimple stable conjugacy classes in 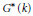${{G}^{*}}\,(k)$ to the analogous set for 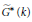$\widetilde{{{G}^{*}}}\,(k)$. If 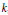$k$ is finite, then our groups are automatically quasisplit, and our result specializes to give a map of semisimple conjugacy classes. Since such classes parametrize packets of irreducible representations of 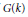$G(k)$ and 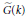$\widetilde{G}\,(k)$, one obtains a mapping of such packets.