We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the Lambek calculus, or noncommutative multiplicative intuitionistic linear logic, extended with iteration, or Kleene star, axiomatised by means of an
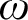$\omega $
-rule, and prove that the derivability problem in this calculus is
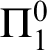$\Pi _1^0$
-hard. This solves a problem left open by Buszkowski (2007), who obtained the same complexity bound for infinitary action logic, which additionally includes additive conjunction and disjunction. As a by-product, we prove that any context-free language without the empty word can be generated by a Lambek grammar with unique type assignment, without Lambek’s nonemptiness restriction imposed (cf. Safiullin, 2007).
