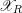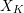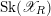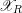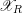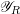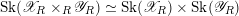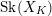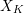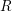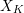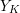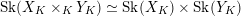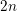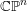We study the problem of how the dual complex of the special fiber of a strict normal crossings degeneration 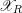 $\mathscr{X}_{R}$ changes under products. We view the dual complex as a skeleton inside the Berkovich space associated to
$\mathscr{X}_{R}$ changes under products. We view the dual complex as a skeleton inside the Berkovich space associated to 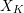 $X_{K}$. Using the Kato fan, we define a skeleton
$X_{K}$. Using the Kato fan, we define a skeleton 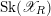 $\text{Sk}(\mathscr{X}_{R})$ when the model
$\text{Sk}(\mathscr{X}_{R})$ when the model 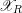 $\mathscr{X}_{R}$ is log-regular. We show that if
$\mathscr{X}_{R}$ is log-regular. We show that if 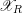 $\mathscr{X}_{R}$ and
$\mathscr{X}_{R}$ and 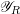 $\mathscr{Y}_{R}$ are log-smooth, and at least one is semistable, then
$\mathscr{Y}_{R}$ are log-smooth, and at least one is semistable, then 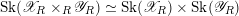 $\text{Sk}(\mathscr{X}_{R}\times _{R}\mathscr{Y}_{R})\simeq \text{Sk}(\mathscr{X}_{R})\times \text{Sk}(\mathscr{Y}_{R})$. The essential skeleton
$\text{Sk}(\mathscr{X}_{R}\times _{R}\mathscr{Y}_{R})\simeq \text{Sk}(\mathscr{X}_{R})\times \text{Sk}(\mathscr{Y}_{R})$. The essential skeleton 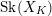 $\text{Sk}(X_{K})$, defined by Mustaţă and Nicaise, is a birational invariant of
$\text{Sk}(X_{K})$, defined by Mustaţă and Nicaise, is a birational invariant of 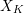 $X_{K}$ and is independent of the choice of
$X_{K}$ and is independent of the choice of 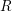 $R$-model. We extend their definition to pairs, and show that if both
$R$-model. We extend their definition to pairs, and show that if both 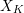 $X_{K}$ and
$X_{K}$ and 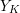 $Y_{K}$ admit semistable models,
$Y_{K}$ admit semistable models, 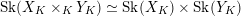 $\text{Sk}(X_{K}\times _{K}Y_{K})\simeq \text{Sk}(X_{K})\times \text{Sk}(Y_{K})$. As an application, we compute the homeomorphism type of the dual complex of some degenerations of hyper-Kähler varieties. We consider both the case of the Hilbert scheme of a semistable degeneration of K3 surfaces, and the generalized Kummer construction applied to a semistable degeneration of abelian surfaces. In both cases we find that the dual complex of the
$\text{Sk}(X_{K}\times _{K}Y_{K})\simeq \text{Sk}(X_{K})\times \text{Sk}(Y_{K})$. As an application, we compute the homeomorphism type of the dual complex of some degenerations of hyper-Kähler varieties. We consider both the case of the Hilbert scheme of a semistable degeneration of K3 surfaces, and the generalized Kummer construction applied to a semistable degeneration of abelian surfaces. In both cases we find that the dual complex of the 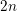 $2n$-dimensional degeneration is homeomorphic to a point,
$2n$-dimensional degeneration is homeomorphic to a point,  $n$-simplex, or
$n$-simplex, or 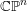 $\mathbb{C}\mathbb{P}^{n}$, depending on the type of the degeneration.
$\mathbb{C}\mathbb{P}^{n}$, depending on the type of the degeneration.