We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We obtain some results on approximate solutions of the generalised linear functional equation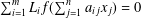 
$\sum _{i=1}^{m}L_{i}f(\sum _{j=1}^{n}a_{ij}x_{j})=0$ for functions mapping a normed space into a normed space. We show that, under suitable assumptions, the approximate solutions are in fact exact solutions. The theorems correspond to and complement recent results on the hyperstability of generalised linear functional equations.
