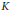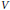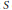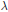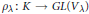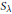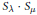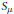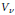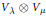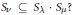This paper aims to lay the foundations for a combinatorial study, via orthogonal functions and intertwining operators, of category 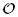 for the rational Cherednik algebra of type G(r, p, n). As a first application, a self-contained and elementary proof of the analogue for the groups G(r, p, n), with r > 1, of Gordon's Theorem (previously Haiman's Conjecture) on the diagonal co-invariant ring is given. No restriction is imposed on p; the result for p ≠ r has been proved by Vale using a technique analogous to Gordon's. Because of the combinatorial application to Haiman's Conjecture, the paper is logically self-contained except for standard facts about complex reflection groups. The main results should be accessible to mathematicians working in algebraic combinatorics who are unfamiliar with the impressive range of ideas used in Gordon's proof of his theorem.
for the rational Cherednik algebra of type G(r, p, n). As a first application, a self-contained and elementary proof of the analogue for the groups G(r, p, n), with r > 1, of Gordon's Theorem (previously Haiman's Conjecture) on the diagonal co-invariant ring is given. No restriction is imposed on p; the result for p ≠ r has been proved by Vale using a technique analogous to Gordon's. Because of the combinatorial application to Haiman's Conjecture, the paper is logically self-contained except for standard facts about complex reflection groups. The main results should be accessible to mathematicians working in algebraic combinatorics who are unfamiliar with the impressive range of ideas used in Gordon's proof of his theorem.

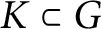
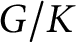
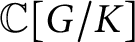
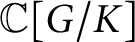
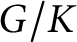
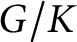
 for the rational Cherednik algebra of type
for the rational Cherednik algebra of type