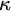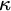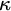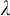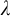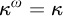1 results
PARTITION OF LARGE SUBSETS OF SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
-
It is known that in an infinite very weakly cancellative semigroup with size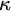
$\kappa $, any central set can be partitioned into 
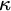$\kappa $ central sets. Furthermore, if 
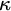$\kappa $ contains 
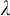$\lambda $ almost disjoint sets, then any central set contains 
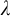$\lambda $ almost disjoint central sets. Similar results hold for thick sets, very thick sets and piecewise syndetic sets. In this article, we investigate three other notions of largeness: quasi-central sets, C-sets, and J-sets. We obtain that the statement applies for quasi-central sets. If the semigroup is commutative, then the statement holds for C-sets. Moreover, if 
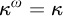$\kappa ^\omega = \kappa $, then the statement holds for J-sets.
