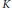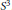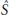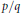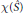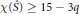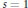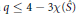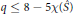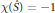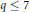Let  $K$ be a knot in
$K$ be a knot in
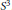 ${{S}^{3}}$
. This paper is devoted to Dehn surgeries which create 3-manifolds containing a closed non-orientable surface
${{S}^{3}}$
. This paper is devoted to Dehn surgeries which create 3-manifolds containing a closed non-orientable surface
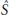 $\hat{S}$
. We look at the slope
$\hat{S}$
. We look at the slope 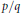 $p/q$ of the surgery, the Euler characteristic
$p/q$ of the surgery, the Euler characteristic
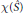 $\mathcal{X}(\hat{S})$
of the surface and the intersection number
$\mathcal{X}(\hat{S})$
of the surface and the intersection number  $s$ between
$s$ between
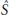 $\hat{S}$
and the core of the Dehn surgery. We prove that if
$\hat{S}$
and the core of the Dehn surgery. We prove that if
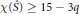 $\mathcal{X}(\hat{S})\,\ge \,15\,-3q$, then
$\mathcal{X}(\hat{S})\,\ge \,15\,-3q$, then 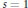 $s\,=\,1$. Furthermore, if
$s\,=\,1$. Furthermore, if 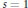 $s\,=\,1$ then
$s\,=\,1$ then
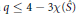 $q\,\le \,4\,-\,3\,\mathcal{X}(\hat{S})$
or
$q\,\le \,4\,-\,3\,\mathcal{X}(\hat{S})$
or  $K$ is cabled and
$K$ is cabled and
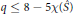 $q\,\le \,8\,-5\mathcal{X}(\hat{S})$
. As consequence, if
$q\,\le \,8\,-5\mathcal{X}(\hat{S})$
. As consequence, if  $K$ is hyperbolic and
$K$ is hyperbolic and
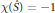 $\mathcal{X}(\hat{S})\,=\,-1$
, then
$\mathcal{X}(\hat{S})\,=\,-1$
, then 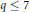 $q\,\le \,7$.
$q\,\le \,7$.