1 results
ON THE SET OF KRONECKER NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 262-270
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
A positive even number is said to be a Maillet number if it can be written as the difference between two primes, and a Kronecker number if it can be written in infinitely many ways as the difference between two primes. It is believed that all even numbers are Kronecker numbers. We study the division and multiplication of Kronecker numbers and show that these numbers are rather abundant. We prove that there is a computable constant k and a set D consisting of at most 720 computable Maillet numbers such that, for any integer n,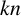
$kn$ can be expressed as a product of a Kronecker number and a Maillet number in D. We also prove that every positive rational number can be written as a ratio of two Kronecker numbers.
