We initiate the program of extending to higher-rank graphs (k-graphs) the geometric classification of directed graph 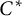 $C^*$
-algebras, as completed in Eilers et al. (2016, Preprint). To be precise, we identify four “moves,” or modifications, one can perform on a k-graph
$C^*$
-algebras, as completed in Eilers et al. (2016, Preprint). To be precise, we identify four “moves,” or modifications, one can perform on a k-graph 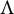 $\Lambda $
, which leave invariant the Morita equivalence class of its
$\Lambda $
, which leave invariant the Morita equivalence class of its 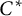 $C^*$
-algebra
$C^*$
-algebra 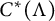 $C^*(\Lambda )$
. These moves—in-splitting, delay, sink deletion, and reduction—are inspired by the moves for directed graphs described by Sørensen (Ergodic Th. Dyn. Syst. 33(2013), 1199–1220) and Bates and Pask (Ergodic Th. Dyn. Syst. 24(2004), 367–382). Because of this, our perspective on k-graphs focuses on the underlying directed graph. We consequently include two new results, Theorem 2.3 and Lemma 2.9, about the relationship between a k-graph and its underlying directed graph.
$C^*(\Lambda )$
. These moves—in-splitting, delay, sink deletion, and reduction—are inspired by the moves for directed graphs described by Sørensen (Ergodic Th. Dyn. Syst. 33(2013), 1199–1220) and Bates and Pask (Ergodic Th. Dyn. Syst. 24(2004), 367–382). Because of this, our perspective on k-graphs focuses on the underlying directed graph. We consequently include two new results, Theorem 2.3 and Lemma 2.9, about the relationship between a k-graph and its underlying directed graph.
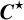 ${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
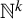 $\mathbb {N}^k$
-actions
$\mathbb {N}^k$
-actions