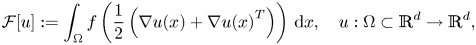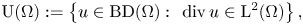1 results
On the relaxation of integral functionals depending on the symmetrized gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 473-508
- Print publication:
- April 2021
-
- Article
- Export citation
-
We prove results on the relaxation and weak* lower semicontinuity of integral functionals of the form
over the space BD(Ω) of functions of bounded deformation or over the Temam–Strang space
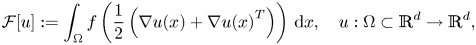$${\cal F}[u]: = \int_\Omega f \left( {\displaystyle{1 \over 2}\left( {\nabla u(x) + \nabla u{(x)}^T} \right)} \right) \,{\rm d}x,\quad u:\Omega \subset {\mathbb R}^d\to {\mathbb R}^d,$$depending on the growth and shape of the integrand f. Such functionals are interesting, for example, in the study of Hencky plasticity and related models.
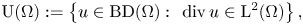$${\rm U}(\Omega ): = \left\{ {u\in {\rm BD}(\Omega ):\;\,{\rm div}\,u\in {\rm L}^2(\Omega )} \right\},$$
