A classic hand-eye system involves hand-eye calibration and robot-world and hand-eye calibration. Insofar as hand-eye calibration can solve only hand-eye transformation, this study aims to determine the robot-world and hand-eye transformations simultaneously based on the robot-world and hand-eye equation. According to whether the rotation part and the translation part of the equation are decoupled, the methods can be divided into separable solutions and simultaneous solutions. The separable solutions solve the rotation part before solving the translation part, so the estimated errors of the rotation will be transferred to the translation. In this study, a method was proposed for calculation with rotation and translation coupling; a closed-form solution based on Kronecker product and an iterative solution based on the Gauss–Newton algorithm were involved. The feasibility was further tested using simulated data and real data, and the superiority was verified by comparison with the results obtained by the available method. Finally, we improved a method that can solve the singularity problem caused by the parameterization of the rotation matrix, which can be widely used in the robot-world and hand-eye calibration. The results show that the prediction errors of rotation and translation based on the proposed method be reduced to 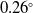 $0.26^\circ$
and
$0.26^\circ$
and 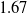 $1.67$
mm, respectively.
$1.67$
mm, respectively.