1 results
Steady-state analysis of a multiserver queue in the Halfin-Whitt regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 548-577
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
-
We consider a multiserver queue in the Halfin-Whitt regime: as the number of servers n grows without a bound, the utilization approaches 1 from below at the rate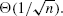
Assuming that the service time distribution is lattice valued with a finite support, we characterize the limiting scaled stationary queue length distribution in terms of the stationary distribution of an explicitly constructed Markov chain. Furthermore, we obtain an explicit expression for the critical exponent for the moment generating function of a limiting stationary queue length. This exponent has a compact representation in terms of three parameters: the amount of spare capacity and the coefficients of variation of interarrival and service times. Interestingly, it matches an analogous exponent corresponding to a single-server queue in the conventional heavy-traffic regime.
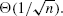Assuming that the service time distribution is lattice valued with a finite support, we characterize the limiting scaled stationary queue length distribution in terms of the stationary distribution of an explicitly constructed Markov chain. Furthermore, we obtain an explicit expression for the critical exponent for the moment generating function of a limiting stationary queue length. This exponent has a compact representation in terms of three parameters: the amount of spare capacity and the coefficients of variation of interarrival and service times. Interestingly, it matches an analogous exponent corresponding to a single-server queue in the conventional heavy-traffic regime.