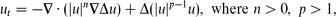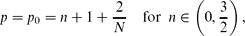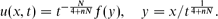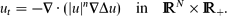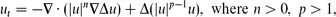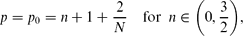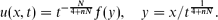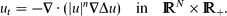We consider the fourth-order thin film equation,
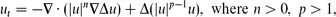 with a stable second-order diffusion term. For the first critical exponent,
with a stable second-order diffusion term. For the first critical exponent,
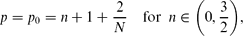 where N ≥ 1 is the space dimension, the Cauchy problem is shown to admit countable continuous branches of source-type self-similar very singular solutions of the form
where N ≥ 1 is the space dimension, the Cauchy problem is shown to admit countable continuous branches of source-type self-similar very singular solutions of the form
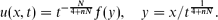 These solutions are inherently oscillatory in nature and will be shown in Part II to be the limit of appropriate free-boundary problem solutions. For p ≠ p0, the set of very singular solutions is shown to be finite and to be consisting of a countable family of branches (in the parameter p) of similarity profiles that originate at a sequence of critical exponents {pl, l ≥ 0}. At p = pl, these branches appear via a non-linear bifurcation mechanism from a countable set of similarity solutions of the second kind of the pure thin film equation
These solutions are inherently oscillatory in nature and will be shown in Part II to be the limit of appropriate free-boundary problem solutions. For p ≠ p0, the set of very singular solutions is shown to be finite and to be consisting of a countable family of branches (in the parameter p) of similarity profiles that originate at a sequence of critical exponents {pl, l ≥ 0}. At p = pl, these branches appear via a non-linear bifurcation mechanism from a countable set of similarity solutions of the second kind of the pure thin film equation
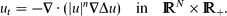 Such solutions are detected by the ‘Hermitian spectral theory’, which allows an analytical n-branching approach. As such, a continuous path as n → 0+ can be constructed from the eigenfunctions of the linear rescaled operator for n = 0, i.e. for the bi-harmonic equation ut = −Δ2u. Numerics are used, wherever appropriate, to support the analysis.
Such solutions are detected by the ‘Hermitian spectral theory’, which allows an analytical n-branching approach. As such, a continuous path as n → 0+ can be constructed from the eigenfunctions of the linear rescaled operator for n = 0, i.e. for the bi-harmonic equation ut = −Δ2u. Numerics are used, wherever appropriate, to support the analysis.