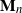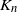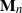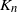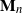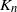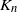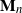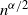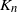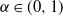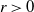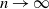We derive large-sample and other limiting distributions of components of the allele frequency spectrum vector, 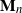$\mathbf{M}_n$, joint with the number of alleles, 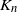$K_n$, from a sample of n genes. Models analysed include those constructed from gamma and $\alpha$-stable subordinators by Kingman (thus including the Ewens model), the two-parameter extension by Pitman and Yor, and a two-parameter version constructed by omitting large jumps from an $\alpha$-stable subordinator. In each case the limiting distribution of a finite number of components of 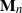$\mathbf{M}_n$ is derived, joint with 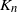$K_n$. New results include that in the Poisson–Dirichlet case, 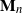$\mathbf{M}_n$ and 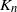$K_n$ are asymptotically independent after centering and norming for 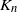$K_n$, and it is notable, especially for statistical applications, that in other cases the limiting distribution of a finite number of components of 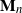$\mathbf{M}_n$, after centering and an unusual 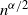$n^{\alpha/2}$ norming, conditional on that of 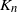$K_n$, is normal.

We derive the large-sample distribution of the number of species in a version of Kingman’s Poisson–Dirichlet model constructed from an $\alpha$ -stable subordinator but with an underlying negative binomial process instead of a Poisson process. Thus it depends on parameters $\alpha\in (0,1)$ from the subordinator and $r>0$ from the negative binomial process. The large-sample distribution of the number of species is derived as sample size $n\to\infty$ . An important component in the derivation is the introduction of a two-parameter version of the Dickman distribution, generalising the existing one-parameter version. Our analysis adds to the range of Poisson–Dirichlet-related distributions available for modeling purposes.