We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this note, we compare the arrival and time stationary distributions of the number of customers in the GI/M/1/n and GI/M/1 queueing systems. We show that, if the inter-arrival c.d.f. H is non-lattice with mean value λ –1, and if the traffic intensity ρ = λμ –1 is strictly less than one, then the convergence rate of the stationary distributions of GI/M/1/n to the corresponding stationary distributions of GI/M/1 is geometric. More-over, the convergence rate can be characterized by the number ω, the unique solution in (0, 1) of the equation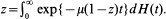 
. A similar result is established for the M/GI/1/n and M/GI/1 queueing systems.
