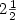1 results
Fast Singular Oscillating Limits and Global Regularity for the 3D Primitive Equations of Geophysics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 34 / Issue 2 / March 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 201-222
- Print publication:
- March 2000
-
- Article
- Export citation
-
Fast singular oscillating limits ofthe three-dimensional "primitive" equations ofgeophysical fluid flows are analyzed.We prove existence on infinite time intervals of regular solutions to the3D "primitive" Navier-Stokes equations for strongstratification (large stratification parameter N).This uniform existence is proven forperiodic or stress-free boundary conditionsfor all domain aspect ratios,including the case of three wave resonances which yield nonlinear " $2\frac{1}{2}$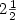
dimensional" limit equations for N → +∞;smoothness assumptions are the same as for localexistence theorems, that is initial data in Hα , α ≥ 3/4.The global existence is proven using techniques ofthe Littlewood-Paley dyadic decomposition.Infinite time regularity for solutions of the3D "primitive" Navier-Stokes equations is obtained by bootstrapping from global regularity of the limit resonantequations and convergence theorems.
