This paper investigates when it is possible for a partial ordering ℙ to force Pk(Λ)\V to be stationary in Vℙ. It follows from a result of Gitik that whenever ℙ adds a new real, then Pk(Λ)\V is stationary in Vℙ for each regular uncountable cardinal κ in Vℙ and all cardinals λ ≥ κ in Vℙ [4], However, a covering theorem of Magidor implies that when no new ω-sequences are added, large cardinals become necessary [7]. The following is equiconsistent with a proper class of ω1-Erdős cardinals: If ℙ is ℵ1-Cohen forcing, then Pk(Λ)\V is stationary in Vℙ, for all regular κ ≥ ℵ2and all λ ≩ κ. The following is equiconsistent with an ω1-Erdős cardinal: If ℙ is ℵ1-Cohen forcing, then 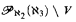 is stationary in Vℙ. The following is equiconsistent with κ measurable cardinals: If ℙ is κ-Cohen forcing, then
is stationary in Vℙ. The following is equiconsistent with κ measurable cardinals: If ℙ is κ-Cohen forcing, then 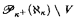 is stationary in Vℙ.
is stationary in Vℙ.

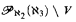 is stationary in
is stationary in 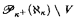 is stationary in
is stationary in 