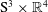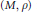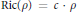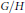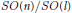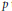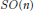2 results
Nearly Parallel G2-structures with Large Symmetry Group
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 December 2019, pp. 339-359
- Print publication:
- April 2021
-
- Article
- Export citation
-
We prove the existence of a one-parameter family of nearly parallel G2-structures on the manifold
$\text{S}^{3}\times \mathbb{R}^{4}$, which are mutually non-isomorphic and invariant under the cohomogeneity one action of the group SU(2)3. This family connects the two locally homogeneous nearly parallel G2-structures that are induced by the homogeneous ones on the sphere S7.
Invariant Einstein Metrics on Some Homogeneous Spaces of Classical Lie Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1213
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
-
A Riemannian manifold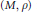
$\left( M,\,\rho \right)$ is called Einstein if the metric 
$\rho $ satisfies the condition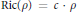 
$\text{Ric}\left( \rho \right)\,=\,c\,\cdot \,\rho $ for some constant 
$c$. This paper is devoted to the investigation of 
$G$-invariant Einstein metrics, with additional symmetries, on some homogeneous spaces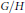 
$G/H$ of classical groups. As a consequence, we obtain new invariant Einstein metrics on some Stiefel manifolds 
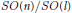$SO\left( n \right)/SO\left( l \right)$. Furthermore, we show that for any positive integer 
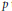$p$ there exists a Stiefel manifold 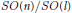$SO\left( n \right)/SO\left( l \right)$ that admits at least 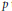$p$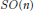
$SO\left( n \right)$-invariant Einstein metrics.
