1 results
Coefficients of ergodicity for stochastically monotone Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 850-860
- Print publication:
- December 1992
-
- Article
- Export citation
-
In this paper we show that to each distance d defined on the finite state space S of a strongly ergodic Markov chain there corresponds a coefficient ρd of ergodicity based on the Wasserstein metric. For a class of stochastically monotone transition matrices P, the infimum over all such coefficients is given by the spectral radius of P – R, where R = limkPk and is attained. This result has a probabilistic interpretation of a control of the speed of convergence of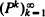
by the metric d and is linked to the second eigenvalue of P.
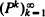by the metric 