In this paper, we decompose
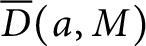 $\overline {D}(a,M)$
into modular and mock modular parts, so that it gives as a straightforward consequencethe celebrated results of Bringmann and Lovejoy on Maass forms. Let
$\overline {D}(a,M)$
into modular and mock modular parts, so that it gives as a straightforward consequencethe celebrated results of Bringmann and Lovejoy on Maass forms. Let
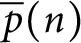 $\overline {p}(n)$
be the number of partitions of n and
$\overline {p}(n)$
be the number of partitions of n and
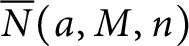 $\overline {N}(a,M,n)$
be the number of overpartitions of n with rank congruent to a modulo M. Motivated by Hickerson and Mortenson, we find and prove a general formula for Dyson’s ranks by considering the deviation of the ranks from the average:
$\overline {N}(a,M,n)$
be the number of overpartitions of n with rank congruent to a modulo M. Motivated by Hickerson and Mortenson, we find and prove a general formula for Dyson’s ranks by considering the deviation of the ranks from the average:
$$ \begin{align*} \overline{D}(a,M) &=\sum\limits_{n=0}^{\infty}\Big(\overline{N}(a,M,n) -\frac{\overline{p}(n)}{M}\Big)q^{n}. \end{align*} $$
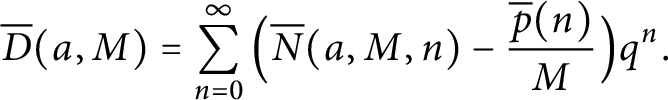
Based on Appell–Lerch sum properties and universal mock theta functions, we obtain the stronger version of the results of Bringmann and Lovejoy.