We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A space has the shrinking property if, for every open cover {Va | a ∈ A}, there is an open cover {Wa | a ∈ A} with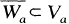 
for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.
