1 results
Borg's Periodicity Theorems for First-Order Self-Adjoint Systems with Complex Potentials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 19 December 2016, pp. 615-633
-
- Article
- Export citation
-
A self-adjoint first-order system with Hermitian π-periodic potential Q(z), integrable on compact sets, is considered. It is shown that all zeros of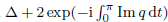
are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which Q(z) is π/2-periodic. Furthermore, the zeros of 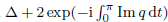are all double zeros if and only if the associated self-adjoint system is unitarily equivalent to one in which Q(z) = σ2Q(z)σ2. Here, Δ denotes the discriminant of the system and σ0, σ2 are Pauli matrices. Finally, it is shown that all instability intervals vanish if and only if Q = rσ0 + qσ2, for some real-valued π-periodic functions r and q integrable on compact sets.
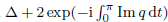are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which 