1 results
Distributions of ballot problem random variables
-
- Journal:
- Advances in Applied Probability / Volume 23 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 01 July 2016, pp. 586-597
- Print publication:
- September 1991
-
- Article
- Export citation
-
Suppose that in a ballot candidate A scores a votes and candidate B scores b votes, and that all the possible voting records are equally probable. Corresponding to the first r votes, let α r and β r be the numbers of votes registered for A and B, respectively. Let p be an arbitrary positive real number. Denote by δ (a, b, p)[δ *(a, b, ρ)] the number of values of r for which the inequality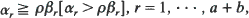
, r = 1, ···, a + b, holds. Heretofore the probability distributions of δand δ* have been derived for only a restricted set of values of a, b, and ρ, although, as pointed out here, they are obtainable for all values of (a, b, ρ) by using a result of Takács (1964). In this paper we present a derivation of the distribution of δ [δ *] whose development, for any (a, b, ρ), leads to both necessary and sufficient conditions for δ [δ *] to have a discrete uniform distribution.
, 
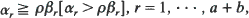