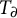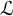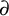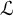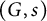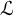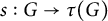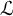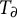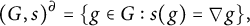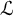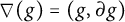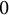1 results
On definable groups and D-groups in certain fields with a generic derivation
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 January 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We continue our study from Peterzil et al. (2022, Preprint, arXiv:2208.08293) of finite-dimensional definable groups in models of the theory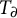
$T_{\partial }$, the model companion of an o-minimal 
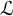${\mathcal {L}}$-theory T expanded by a generic derivation 
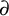$\partial $ as in Fornasiero and Kaplan (2021, Journal of Mathematical Logic 21, 2150007).We generalize Buium’s notion of an algebraic D-group to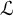
${\mathcal {L}}$-definable D-groups, namely 
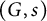$(G,s)$, where G is an 
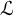${\mathcal {L}}$-definable group in a model of T, and 
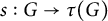$s:G\to \tau (G)$ is an 
${\mathcal {L}}$-definable group section. Our main theorem says that every definable group of finite dimension in a model of 
$T_\partial $ is definably isomorphic to a group of the form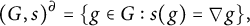 
$$ \begin{align*}(G,s)^\partial=\{g\in G:s(g)=\nabla g\},\end{align*} $$for some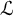
${\mathcal {L}}$-definable D-group 
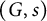$(G,s)$ (where 
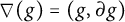$\nabla (g)=(g,\partial g)$).We obtain analogous results when T is either the theory of p-adically closed fields or the theory of pseudo-finite fields of characteristic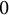
$0$.
