In a recent paper, Bondarko [Weight structures vs. t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general), Preprint (2007), 0704.4003] defined the notion of weight structure, and proved that the category DMgm(k) of geometrical motives over a perfect field k, as defined and studied by Voevodsky, Suslin and Friedlander [Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000)], is canonically equipped with such a structure. Building on this result, and under a condition on the weights avoided by the boundary motive [J. Wildeshaus, The boundary motive: definition and basic properties, Compositio Math. 142 (2006), 631–656], we describe a method to construct intrinsically in DMgm(k) a motivic version of interior cohomology of smooth, but possibly non-projective schemes. In a sequel to this work [J. Wildeshaus, On the interior motive of certain Shimura varieties: the case of Hilbert–Blumenthal varieties, Preprint (2009), 0906.4239], this method will be applied to Shimura varieties.
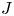 $J$-invariant over splitting fields of Tits algebras
$J$-invariant over splitting fields of Tits algebras

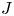
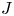
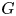
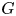
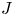
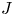
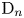
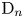
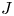
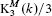 . We also establish a motivic isomorphism between two anisotropic non-isomorphic projective homogeneous varieties of type F
. We also establish a motivic isomorphism between two anisotropic non-isomorphic projective homogeneous varieties of type F