The study of simple solar energy storage models leads to the question of analyzing the equilibrium distribution of Markov chains (Harris chains), for which the state at epoch (n + 1) (i.e. the temperature of the storage tank) depends on the state at epoch n and on a controlled input, acceptance of which entails a further decrease of the temperature level. Here we study the model where the input is exponentially distributed. For all values of the parameters involved an explicit expression for the equilibrium distribution of the Markov chain is derived, and from this we calculate, as one of the possible applications, the exact values of the mean of this equilibrium distribution.

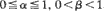 , 0<
, 0<