We study bundles on projective spaces that have vanishing lower cohomologies using their short minimal free resolutions. We partition the moduli 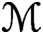 $\mathcal{M}$
according to the Hilbert function H and classify all possible Hilbert functions H of such bundles. For each H, we describe a stratification of
$\mathcal{M}$
according to the Hilbert function H and classify all possible Hilbert functions H of such bundles. For each H, we describe a stratification of
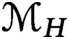 $\mathcal{M}_H$
by quotients of rational varieties. We show that the closed strata form a graded lattice given by the Betti numbers.
$\mathcal{M}_H$
by quotients of rational varieties. We show that the closed strata form a graded lattice given by the Betti numbers.
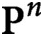 $\textbf{P}^n$
with vanishing lower cohomologies
$\textbf{P}^n$
with vanishing lower cohomologies