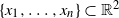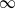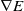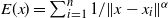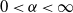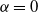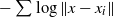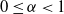1 results
Random growth via gradient flow aggregation
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
-
We introduce gradient flow aggregation, a random growth model. Given existing particles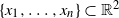
$\{x_1,\ldots,x_n\} \subset \mathbb{R}^2$, a new particle arrives from a random direction at 
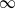$\infty$ and flows in direction of the vector field 
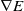$\nabla E$ where 
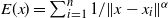$ E(x) = \sum_{i=1}^{n}{1}/{\|x-x_i\|^{\alpha}}$, 
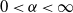$0 < \alpha < \infty$. The case 
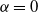$\alpha = 0$ refers to the logarithmic energy 
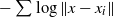${-}\sum\log\|x-x_i\|$. Particles stop once they are at distance 1 from one of the existing particles, at which point they are added to the set and remain fixed for all time. We prove, under a non-degeneracy assumption, a Beurling-type estimate which, via Kesten’s method, can be used to deduce sub-ballistic growth for 
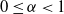$0 \leq \alpha < 1$, 
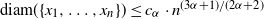$\text{diam}(\{x_1,\ldots,x_n\}) \leq c_{\alpha} \cdot n^{({3 \alpha +1})/({2\alpha + 2})}$. This is optimal when 
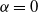$\alpha = 0$. The case 
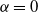$\alpha = 0$ leads to a ‘round’ full-dimensional tree. The larger the value of 
$\alpha$, the sparser the tree. Some instances of the higher-dimensional setting are also discussed.
