Three related estimators are considered for the parametrized spectral density of a discrete-time process X(n), n = 1, 2, · · ·, when observations are not available for all the values n = 1(1)N. Each of the estimators is obtained by maximizing a frequency domain approximation to a Gaussian likelihood, although they do not appear to be the most efficient estimators available because they do not fully utilize the information in the process a(n) which determines whether X(n) is observed or missed. One estimator, called M3, assumes that the second-order properties of a(n) are known; another, M2, lets these be known only up to an unknown parameter vector; the third, M1, requires no model for a(n). Under representative sets of conditions, which allow for both deterministic and stochastic a(n), the strong consistency and asymptotic normality of M1, M2, and M3 are established. The conditions needed for consistency when X(n) is an autoregressive moving-average process are discussed in more detail. It is also shown that in general M1 and M3 are equally efficient asymptotically and M2 is never more efficient, and may be less efficient, than M1 and M3.

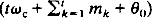 , where the message process {
, where the message process {