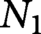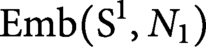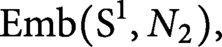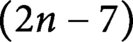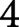Suppose that $N_1$ and $N_2$ are closed smooth manifolds of dimension n that are homeomorphic. We prove that the spaces of smooth knots, $ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N_1)$ and $ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N_2),$ have the same homotopy $(2n-7)$ -type. In the four-dimensional case, this means that the spaces of smooth knots in homeomorphic $4$ -manifolds have sets 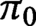$\pi _0$ of components that are in bijection, and the corresponding path components have the same fundamental groups 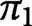$\pi _1$ . 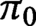The result about $\pi _0$ is well-known and elementary, but the result about 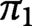$\pi _1$ appears to be new. The result gives a negative partial answer to a question of Oleg Viro. Our proof uses the Goodwillie–Weiss embedding tower. We give a new model for the quadratic stage of the Goodwillie–Weiss tower, and prove that the homotopy type of the quadratic approximation of the space of knots in N does not depend on the smooth structure on N. Our results also give a lower bound on $\pi _2 \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N)$ . We use our model to show that for every choice of basepoint, each of the homotopy groups, 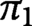$\pi _1$ and 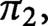$\pi _2,$ of 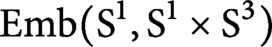$ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, \mathrm {S}^1\times \mathrm {S}^3)$ contains an infinitely generated free abelian group.

Building upon our earlier work with M. C. Hughes, we construct many new smooth structures on closed simply connected nonspin $4$ -manifolds with positive signature. We also provide numerical and asymptotic upper bounds on the function $\lambda (\sigma )$ that was defined in our earlier work.

We construct an infinite family of simply connected, pairwise nondiffeomorphic 4-manifolds, all homeomorphic to $3{\mathbb {CP}}^2 \# 9 {\overline {{\mathbb C}{\mathbb P}^2}}$. Similar ideas provide examples of 4-manifolds with $b_2^+=3$, $b_2^-=8$, vanishing first homology and nontrivial Seiberg–Witten invariants.