We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A famous conjecture of Hopf states that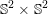 
$\mathbb{S}^{2}\times \mathbb{S}^{2}$ does not admit a Riemannian metric with positive sectional curvature. In this article, we prove that no manifold product 
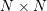$N\times N$ can carry a metric of positive sectional curvature admitting a certain degree of torus symmetry.
