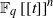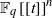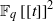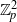In a recent paper of Ellenberg, Oberlin, and Tao [The Kakeya set and maximal conjectures for algebraic varieties over finite fields. Mathematika 56 (2010), 1–25], the authors asked whether there are Besicovitch phenomena in ${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{n} $. In this paper, we answer their question in the affirmative by explicitly constructing a Kakeya set of measure zero in ${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{n} $. Furthermore, we prove that any Kakeya set in ${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{2} $ or ${ \mathbb{Z} }_{p}^{2} $ is of Minkowski dimension 2.

The natural geometric setting of quadrics commuting with a Hermitian surface of ${\rm PG}(3,q^2)$, q odd, is adopted and a hemisystem on the Hermitian surface ${\cal H}(3,q^2)$ admitting the group $\mathrm{{P}}\Omega^-(4,q)$ is constructed, yielding a partial quadrangle ${\rm PQ}((q-1)/2,q^2,(q-1)^2/2)$ and a strongly regular graph srg$((q^3+1)(q+1)/2,(q^2+1)(q-1)/2,(q-3)/2,(q-1)^2/2)$. For $q>3$, no partial quadrangle or strongly regular graph with these parameters was previously known, whereas when $q=3$, this is the Gewirtz graph. Thas conjectured that there are no hemisystems on ${\cal H}(3,q^2)$ for $q>3$, so these are counterexamples to his conjecture. Furthermore, a hemisystem on ${\cal H}(3,25)$ admitting $3.A_7.2$ is constructed. Finally, special sets (after Shult) and ovoids on ${\cal H}(3,q^2)$ are investigated.