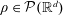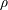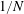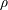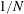We consider a multimarginal transport problem with repulsive cost, where the marginals are all equal to a fixed probability $\unicode[STIX]{x1D70C}\in {\mathcal{P}}(\mathbb{R}^{d})$. We prove that, if the concentration of $\unicode[STIX]{x1D70C}$ is less than $1/N$, then the problem has a solution of finite cost. The result is sharp, in the sense that there exists $\unicode[STIX]{x1D70C}$ with concentration $1/N$ for which the cost is infinite.

Minimizing movements are investigated for an energy which is the superposition of a convex functional and fast small oscillations. Thus a minimizing movement scheme involves a temporal parameter τ and a spatial parameter ε, with τ describing the time step and the frequency of the oscillations being proportional to 1/ε. The extreme cases of fast time scales τ ≪ ε and slow time scales ε ≪ τ have been investigated in [4]. In this paper, the intermediate (critical) case of finite ratio ε/τ > 0 is studied. It is shown that a pinning threshold exists, with initial data below the threshold being a fixed point of the dynamics. A characterization of the pinning threshold is given. For initial data above the pinning threshold, the equation and velocity describing the homogenized motion are determined.

Let $\Omega \subset \R^2$ be a bounded Lipschitz domain and let \[ F: \Omega \times {\mathbb R}_{+}^{2 \times 2} \longrightarrow {\mathbb R} \] be a Carathèodory integrand such that $F\left(x, \cdot\right)$ is polyconvex for ${\mathcal L}^2$-a.e. $x \in \Omega$. Moreover assume that $F$ is bounded from below and satisfies the condition $F\left(x, \xi\right) \searrow \infty$ as $\det \xi \searrow 0$ for ${\mathcal L}^2$-a.e. $x \in \Omega$. The paper describes the effect of domain topology on the existence and multiplicity of strong local minimizers of the functional \[ {\mathbb F} \left[u\right] := \int_{\Omega } F\left(x, \nabla u\left(x\right)\right) \, dx,\] where the map $u$ lies in the Sobolev space $W_{\rm {id}}^{1,p} (\Omega, {\mathbb R}^2)$ with $p \geqslant 2$ and satisfies the pointwise condition $\det \nabla u\left(x\right) >0$ for ${\mathcal L}^2$-a.e. $x \in \Omega$. The question is settled by establishing that ${\mathbb F}\left[\cdot\right]$ admits a set of strong local minimizers on {W^{1,p}_{\rm{id}}(\Omega, {\mathbb R}^2)} that can be indexed by the group $\Pn \oplus \Z^n$, the direct sum of Artin's pure braid group on $n$ strings and $n$ copies of the infinite cyclic group. The dependence on the domain topology is through the number of holes $n$ in $\Omega$ and the different mechanisms that give rise to such local minimizers are fully exploited by this particular representation.