A set in a metric space is called a Čebyšev set if it has a unique “nearest neighbour” to each point of the space. In this paper we generalize this notion, defining a set to be Čebyšev relative to another set if every point in the second set has a unique “nearest neighbour” in the first. We are interested in Čebyšev sets in some hyperspaces over 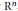${{\text{R}}^{n}}$, endowed with the Hausdorff metric, mainly the hyperspaces of compact sets, compact convex sets, and strictly convex compact sets.

We present some new classes of Čebyšev and relatively Čebyšev sets in various hyperspaces. In particular, we show that certain nested families of sets are Čebyšev. As these families are characterized purely in terms of containment,without reference to the semi-linear structure of the underlyingmetric space, their properties differ markedly from those of known Čebyšev sets.

Let Un be an n-dimensional subspace of C[0, 1]. We prove that if n ≥ 2, and Un contains a function which is strictly positive on (0, 1), then there exists an f ∈ C[0, 1] which has more than one best one-sided L '-approximation from Un. We also characterize those Un with the property that each f ∈ C[0, 1] has a unique best one-sided L1(w)-approximation from Un with respect to every strictly positive continuous weight function w.