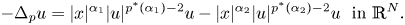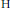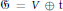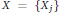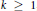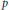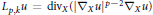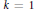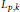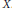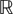Let 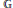 $\mathbb{G}$ be a step-two nilpotent group of
$\mathbb{G}$ be a step-two nilpotent group of 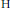 $\text{H}$-type with Lie algebra
$\text{H}$-type with Lie algebra 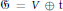 $\mathfrak{G}\,=\,V\,\oplus \,\text{t}$. We define a class of vector fields
$\mathfrak{G}\,=\,V\,\oplus \,\text{t}$. We define a class of vector fields 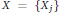 $X\,=\,\left\{ {{X}_{j}} \right\}$ on
$X\,=\,\left\{ {{X}_{j}} \right\}$ on 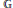 $\mathbb{G}$ depending on a real parameter
$\mathbb{G}$ depending on a real parameter 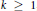 $k\,\ge \,1$, and we consider the corresponding
$k\,\ge \,1$, and we consider the corresponding 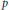 $p$-Laplacian operator
$p$-Laplacian operator 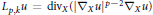 ${{L}_{p,\,k}}u\,=\,di{{v}_{X}}\left( {{\left| {{\nabla }_{X}}u \right|}^{p-2}}{{\nabla }_{X}}u \right)$. For
${{L}_{p,\,k}}u\,=\,di{{v}_{X}}\left( {{\left| {{\nabla }_{X}}u \right|}^{p-2}}{{\nabla }_{X}}u \right)$. For 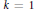 $k\,=\,1$ the vector fields
$k\,=\,1$ the vector fields 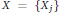 $X\,=\,\left\{ {{X}_{j}} \right\}$ are the left invariant vector fields corresponding to an orthonormal basis of
$X\,=\,\left\{ {{X}_{j}} \right\}$ are the left invariant vector fields corresponding to an orthonormal basis of  $V$; for
$V$; for 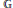 $\mathbb{G}$ being the Heisenberg group the vector fields are the Greiner fields. In this paper we obtain the fundamental solution for the operator
$\mathbb{G}$ being the Heisenberg group the vector fields are the Greiner fields. In this paper we obtain the fundamental solution for the operator 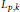 ${{L}_{p,\,k}}$ and as an application, we get a Hardy type inequality associated with
${{L}_{p,\,k}}$ and as an application, we get a Hardy type inequality associated with 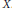 $X$.
$X$.
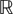 N+
N+