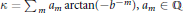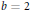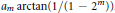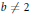Constants with formulae of the form treated by D. Bailey, P. Borwein, and S. Plouffe ($b$ formulae to a given base $b$) have interesting computational properties, such as allowing single digits in their base $b$ expansion to be independently computed, and there are hints that they should be normal numbers, i.e., that their base $b$ digits are randomly distributed. We study a formally limited subset of BBP formulae, which we call Machin-type BBP formulae, for which it is relatively easy to determine whether or not a given constant $K$ has a Machin-type BBP formula. In particular, given $b\,\in \,\mathbb{N},\,b\,>\,2,\,b$ not a proper power, a $b$-ary Machin-type BBP arctangent formula for $K$ is a formula of the form 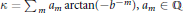$k\,=\,{{\Sigma }_{m}}\,{{a}_{m}}\,\arctan \,(-{{b}^{-m}}),\,{{a}_{m}}\,\in \,\mathbb{Q}$ , while when 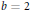$b\,=\,2$, we also allow terms of the form 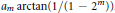${{a}_{m}}\,\arctan \,(1/1\,-\,{{2}^{m}}))$ . Of particular interest, we show that $\pi$ has no Machin-type BBP arctangent formula when 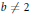$b\,\ne \,2$. To the best of our knowledge, when there is no Machin-type BBP formula for a constant then no BBP formula of any form is known for that constant.