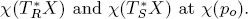We develop some symplectic techniques to control the behavior under symplectic transformation of analytic discs A of X = ℂn tangent to a real generic submanifold R and contained in a wedge with edge R.
We show that if A* is a lift of A to T* X and if χ is a symplectic transformation between neighborhoods of po and qo, then A is orthogonal to po if and only if Ã:= πχA* is orthogonal to qo. Also we give the (real) canonical form of the couples of hypersurfaces of ℝ2n ⋍ ℂn whose conormal bundles have clean intersection. This generalizes [10] to general dimension of intersection.
Combining this result with the quantized action on sheaves of the “tuboidal” symplectic transformation, we show the following: If R, S are submanifolds of X with R ⊂ S and 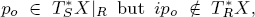 then the conditions
then the conditions 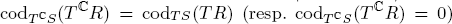 can be characterized as opposite inclusions for the couple of closed half-spaces with conormal bundles
can be characterized as opposite inclusions for the couple of closed half-spaces with conormal bundles 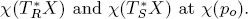
In §3 we give some partial applications of the above result to the analytic hypoellipticity of CR hyperfunctions on higher codimensional manifolds by the aid of discs (cf. [2], [3] as for the case of hypersurfaces).


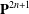


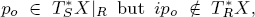 then the conditions
then the conditions 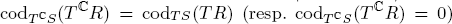 can be characterized as opposite inclusions for the couple of closed half-spaces with conormal bundles
can be characterized as opposite inclusions for the couple of closed half-spaces with conormal bundles