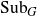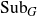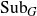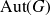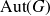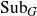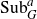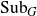For a locally compact metrisable group G, we study the action of ${\rm Aut}(G)$ on ${\rm Sub}_G$ , the set of closed subgroups of G endowed with the Chabauty topology. Given an automorphism T of G, we relate the distality of the T-action on ${\rm Sub}_G$ with that of the T-action on G under a certain condition. If G is a connected Lie group, we characterise the distality of the T-action on ${\rm Sub}_G$ in terms of compactness of the closed subgroup generated by T in ${\rm Aut}(G)$ under certain conditions on the center of G or on T as follows: G has no compact central subgroup of positive dimension or T is unipotent or T is contained in the connected component of the identity in ${\rm Aut}(G)$ . Moreover, we also show that a connected Lie group G acts distally on ${\rm Sub}_G$ if and only if G is either compact or it is isomorphic to a direct product of a compact group and a vector group. All the results on the Lie groups mentioned above hold for the action on ${\rm Sub}^a_G$ , a subset of ${\rm Sub}_G$ consisting of closed abelian subgroups of G.

For a locally compact group G, we study the distality of the action of automorphisms T of G on SubG, the compact space of closed subgroups of G endowed with the Chabauty topology. For a certain class of discrete groups G, we show that T acts distally on SubG if and only if Tn is the identity map for some 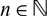$n\in\mathbb N$ . As an application, we get that for a T-invariant lattice Γ in a simply connected nilpotent Lie group G, T acts distally on SubG if and only if it acts distally on SubΓ. This also holds for any closed T-invariant co-compact subgroup Γ in G. For a lattice Γ in a simply connected solvable Lie group, we study conditions under which its automorphisms act distally on SubΓ. We construct an example highlighting the difference between the behaviour of automorphisms on a lattice in a solvable Lie group and that in a nilpotent Lie group. We also characterise automorphisms of a lattice Γ in a connected semisimple Lie group which act distally on SubΓ. For torsion-free compactly generated nilpotent (metrisable) groups G, we obtain the following characterisation: T acts distally on SubG if and only if T is contained in a compact subgroup of Aut(G). Using these results, we characterise the class of such groups G which act distally on SubG. We also show that any compactly generated distal group G is Lie projective.

In this note, we show that results of U. Baumgartner and G. A. Willis concerning contraction groups of automorphisms of metrizable totally disconnected, locally compact groups remain valid also in the non-metrizable case, if one restricts attention to automorphisms for which small tidy subgroups exist.

An explicit description of a hyperbolic canonical coordinate system for an expansive automorphism of a compact connected abelian group is given. These dynamical systems are factors of subshifts of finite type. Some properties of the associated crossed product C*-algebra are discussed. In these examples, the C* -algebras of Ruelle are crossed product algebras.