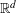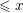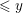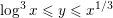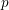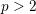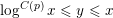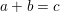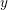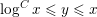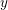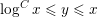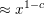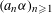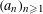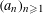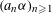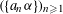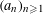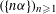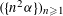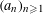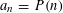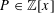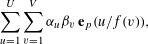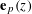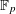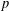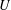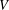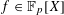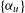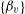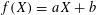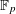Following the work of Chevalley and Warning, Ax obtained a bound on the $p$-divisibility of exponential sums involving multi-variable polynomials of fixed degree $d$ over a finite field of characteristic $p$. This bound was subsequently improved by Katz. More recently, Moreno and Moreno, and Adolphson and Sperber, derived bounds that in many instances improved upon the Ax–Katz result. Here we derive a tight bound on the $p$-divisibility of the exponential sums. While exact computation of this bound requires the solution of a system of modular equations, approximations are provided which in several classes of examples, improve on the results of Chevalley and Warning, Ax and Katz, Adolphson and Sperber, and Moreno and Moreno. All of the above results readily translate into bounds on the $p$-divisibility of the number of zeros of multi-variable polynomials.
An important consequence of one of our main results is a method to find classes of examples for which bounds on divisibility of the number of solutions of a system of polynomial equations over finite fields are tight. In particular, we give classes of examples for which the Moreno–Moreno bound is tight.
It is important to note that we have also found applications of our results to coding theory (computation of the covering radius of certain codes) and to Waring's problem over finite fields. These will be described elsewhere.
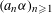 $(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES
$(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES 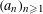 $(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH
$(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH