We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give topological characterizations of filters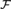 
${\cal F}$ on ω such that the Mathias forcing 
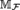${M_{\cal F}}$ adds no dominating reals or preserves ground model unbounded families. This allows us to answer some questions of Brendle, Guzmán, Hrušák, Martínez, Minami, and Tsaban.
